Graph algorithms are a set of instructions that traverse (visits nodes of a) graph.
Some algorithms are used to find a specific node or the path between two given nodes.
Why Graph Algorithms are Important
Graphs are very useful data structures which can be to model various problems. These algorithms have direct applications on Social Networking sites, State Machine modeling and many more.
Some Common Graph Algorithms
Some of the most common graph algorithms are:
Bellman Ford’s Algorithm
Bellman Ford’s algorithm is a shortest path finding algorithm for graphs that can have negative weights. Bellman ford’s algorithm is also great for detecting negative weight cycles as the algorithm converges to an optimal solution in O(V*E) steps. If the resultant is not optimal, then graph contains a negative weight cycle.
Here is an implementation in Python,
infinity = 1e10
def bellman_ford(graph, start, end):
num_vertices = graph.get_num_vertices()
edges = graph.get_edges()
distance = [infinity for vertex in range(num_vertices)]
previous = [None for vertex in range(num_vertices)]
distance[start] = 0
for i range(end+1):
for (u, v) in edges:
if distance[v] > distance[u] + graph.get_weight(u, v):
distance[v] = distance[u] + graph.get_weight(u, v)
previous[v] = u
for (u,v) in edges:
if distance[v] > distance[u] + graph.get_weight(u, v):
raise NegativeWeightCycleError()
return distance, previous
# 'distance' is the distance from start to that node in the shortest path, useful for printing the shortest distance.
# Previous is an array that tells the node that comes previous to current, useful for printing out the path.
Depth First Search (DFS)
Depth First Search is one of the most simple graph algorithms. It traverses the graph by first checking the current node and then moving to one of its sucessors to repeat the process. If the current node has no sucessor to check, we move back to its predecessor and the process continues (by moving to another sucessor). If the solution is found the search stops.
Visualisation

Implementation (C++14)
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
class Graph{
int v; // number of vertices
// pointer to a vector containing adjacency lists
vector < int > *adj;
public:
Graph(int v); // Constructor
// function to add an edge to graph
void add_edge(int v, int w);
// prints dfs traversal from a given source `s`
void dfs();
void dfs_util(int s, vector < bool> &visited);
};
Graph::Graph(int v){
this -> v = v;
adj = new vector < int >[v];
}
void Graph::add_edge(int u, int v){
adj[u].push_back(v); // add v to u’s list
adj[v].push_back(v); // add u to v's list (remove this statement if the graph is directed!)
}
void Graph::dfs(){
// visited vector - to keep track of nodes visited during DFS
vector < bool > visited(v, false); // marking all nodes/vertices as not visited
for(int i = 0; i < v; i++)
if(!visited[i])
dfs_util(i, visited);
}
// notice the usage of call-by-reference here!
void Graph::dfs_util(int s, vector < bool > &visited){
// mark the current node/vertex as visited
visited[s] = true;
// output it to the standard output (screen)
cout << s << " ";
// traverse its adjacency list and recursively call dfs_util for all of its neighbours!
// (only if the neighbour has not been visited yet!)
for(vector < int > :: iterator itr = adj[s].begin(); itr != adj[s].end(); itr++)
if(!visited[*itr])
dfs_util(*itr, visited);
}
int main()
{
// create a graph using the Graph class we defined above
Graph g(4);
g.add_edge(0, 1);
g.add_edge(0, 2);
g.add_edge(1, 2);
g.add_edge(2, 0);
g.add_edge(2, 3);
g.add_edge(3, 3);
cout << "Following is the Depth First Traversal of the provided graph"
<< "(starting from vertex 0): ";
g.dfs();
// output would be: 0 1 2 3
return 0;
}
Evaluation
Space Complexity: O(n)
Worse Case Time Complexity: O(n) Depth First Search is complete on a finite set of nodes. I works better on shallow trees.
Implementation of DFS in C++
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
struct Graph{
int v;
bool **adj;
public:
Graph(int vcount);
void addEdge(int u,int v);
void deleteEdge(int u,int v);
vector<int> DFS(int s);
void DFSUtil(int s,vector<int> &dfs,vector<bool> &visited);
};
Graph::Graph(int vcount){
this->v = vcount;
this->adj=new bool*[vcount];
for(int i=0;i<vcount;i++)
this->adj[i]=new bool[vcount];
for(int i=0;i<vcount;i++)
for(int j=0;j<vcount;j++)
adj[i][j]=false;
}
void Graph::addEdge(int u,int w){
this->adj[u][w]=true;
this->adj[w][u]=true;
}
void Graph::deleteEdge(int u,int w){
this->adj[u][w]=false;
this->adj[w][u]=false;
}
void Graph::DFSUtil(int s, vector<int> &dfs, vector<bool> &visited){
visited[s]=true;
dfs.push_back(s);
for(int i=0;i<this->v;i++){
if(this->adj[s][i]==true && visited[i]==false)
DFSUtil(i,dfs,visited);
}
}
vector<int> Graph::DFS(int s){
vector<bool> visited(this->v);
vector<int> dfs;
DFSUtil(s,dfs,visited);
return dfs;
}
Floyd Warshall Algorithm
Floyd Warshall algorithm is a great algorithm for finding shortest distance between all vertices in graph. It has a very concise algorithm and O(V^3) time complexity (where V is number of vertices). It can be used with negative weights, although negative weight cycles must not be present in the graph.
Evaluation
Space Complexity: O(V^2)
Worse Case Time Complexity: O(V^3)
Python implementation
# A large value as infinity
inf = 1e10
def floyd_warshall(weights):
V = len(weights)
distance_matrix = weights
for k in range(V):
next_distance_matrix = [list(row) for row in distance_matrix] # make a copy of distance matrix
for i in range(V):
for j in range(V):
# Choose if the k vertex can work as a path with shorter distance
next_distance_matrix[i][j] = min(distance_matrix[i][j], distance_matrix[i][k] + distance_matrix[k][j])
distance_matrix = next_distance_matrix # update
return distance_matrix
# A graph represented as Adjacency matrix
graph = [
[0, inf, inf, -3],
[inf, 0, inf, 8],
[inf, 4, 0, -2],
[5, inf, 3, 0]
]
print(floyd_warshall(graph))
Breadth First Search (BFS)
Breadth First Search is one of the most simple graph algorithms. It traverses the graph by first checking the current node and then expanding it by adding its successors to the next level. The process is repeated for all nodes in the current level before moving to the next level. If the solution is found the search stops.
Visualisation
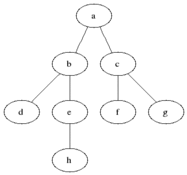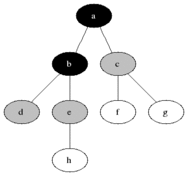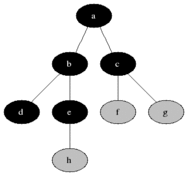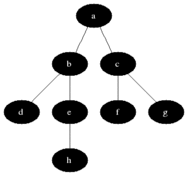
Evaluation
Space Complexity: O(n)
Worse Case Time Complexity: O(n)
Breadth First Search is complete on a finite set of nodes and optimal if the cost of moving from one node to another is constant.
C++ code for BFS implementation
// Program to print BFS traversal from a given
// source vertex. BFS(int s) traverses vertices
// reachable from s.
#include<iostream>
#include <list>
using namespace std;
// This class represents a directed graph using
// adjacency list representation
class Graph
{
int V; // No. of vertices
// Pointer to an array containing adjacency
// lists
list<int> *adj;
public:
Graph(int V); // Constructor
// function to add an edge to graph
void addEdge(int v, int w);
// prints BFS traversal from a given source s
void BFS(int s);
};
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w); // Add w to v’s list.
}
void Graph::BFS(int s)
{
// Mark all the vertices as not visited
bool *visited = new bool[V];
for(int i = 0; i < V; i++)
visited[i] = false;
// Create a queue for BFS
list<int> queue;
// Mark the current node as visited and enqueue it
visited[s] = true;
queue.push_back(s);
// 'i' will be used to get all adjacent
// vertices of a vertex
list<int>::iterator i;
while(!queue.empty())
{
// Dequeue a vertex from queue and print it
s = queue.front();
cout << s << " ";
queue.pop_front();
// Get all adjacent vertices of the dequeued
// vertex s. If a adjacent has not been visited,
// then mark it visited and enqueue it
for (i = adj[s].begin(); i != adj[s].end(); ++i)
{
if (!visited[*i])
{
visited[*i] = true;
queue.push_back(*i);
}
}
}
}
// Driver program to test methods of graph class
int main()
{
// Create a graph given in the above diagram
Graph g(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);
cout << "Following is Breadth First Traversal "
<< "(starting from vertex 2) \n";
g.BFS(2);
return 0;
}
Dijkstra’s Algorithm
Dijkstra’s Algorithm is a graph algorithm presented by E.W. Dijkstra. It finds the single source shortest path in a graph with non-negative edges.(why?)
We create 2 arrays : visited and distance, which record whether a vertex is visited and what is the minimum distance from the source vertex respectively. Initially visited array is assigned as false and distance as infinite.
We start from the source vertex. Let the current vertex be u and its adjacent vertices be v. Now for every v which is adjacent to u, the distance is updated if it has not been visited before and the distance from u is less than its current distance. Then we select the next vertex with the least distance and which has not been visited.
Priority Queue is often used to meet this last requirement in the least amount of time. Below is an implementation of the same idea using priority queue in Java.
import java.util.*;
public class Dijkstra {
class Graph {
LinkedList<Pair<Integer>> adj[];
int n; // Number of vertices.
Graph(int n) {
this.n = n;
adj = new LinkedList[n];
for(int i = 0;i<n;i++) adj[i] = new LinkedList<>();
}
// add a directed edge between vertices a and b with cost as weight
public void addEdgeDirected(int a, int b, int cost) {
adj[a].add(new Pair(b, cost));
}
public void addEdgeUndirected(int a, int b, int cost) {
addEdgeDirected(a, b, cost);
addEdgeDirected(b, a, cost);
}
}
class Pair<E> {
E first;
E second;
Pair(E f, E s) {
first = f;
second = s;
}
}
// Comparator to sort Pairs in Priority Queue
class PairComparator implements Comparator<Pair<Integer>> {
public int compare(Pair<Integer> a, Pair<Integer> b) {
return a.second - b.second;
}
}
// Calculates shortest path to each vertex from source and returns the distance
public int[] dijkstra(Graph g, int src) {
int distance[] = new int[g.n]; // shortest distance of each vertex from src
boolean visited[] = new boolean[g.n]; // vertex is visited or not
Arrays.fill(distance, Integer.MAX_VALUE);
Arrays.fill(visited, false);
PriorityQueue<Pair<Integer>> pq = new PriorityQueue<>(100, new PairComparator());
pq.add(new Pair<Integer>(src, 0));
distance[src] = 0;
while(!pq.isEmpty()) {
Pair<Integer> x = pq.remove(); // Extract vertex with shortest distance from src
int u = x.first;
visited[u] = true;
Iterator<Pair<Integer>> iter = g.adj[u].listIterator();
// Iterate over neighbours of u and update their distances
while(iter.hasNext()) {
Pair<Integer> y = iter.next();
int v = y.first;
int weight = y.second;
// Check if vertex v is not visited
// If new path through u offers less cost then update distance array and add to pq
if(!visited[v] && distance[u]+weight<distance[v]) {
distance[v] = distance[u]+weight;
pq.add(new Pair(v, distance[v]));
}
}
}
return distance;
}
public static void main(String args[]) {
Dijkstra d = new Dijkstra();
Dijkstra.Graph g = d.new Graph(4);
g.addEdgeUndirected(0, 1, 2);
g.addEdgeUndirected(1, 2, 1);
g.addEdgeUndirected(0, 3, 6);
g.addEdgeUndirected(2, 3, 1);
g.addEdgeUndirected(1, 3, 3);
int dist[] = d.dijkstra(g, 0);
System.out.println(Arrays.toString(dist));
}
}
Ford Fulkerson algorithm
Ford Fulkerson’s algorithm solves the maximum flow graph problem. It finds the best organisation of flow through the edges of graphs such that you get maximum flow out on the other end. The source has a specific rate of input and each edge has a weight associated with it which is the maximum substance that can be passed through that edge.
Ford Fulkerson algorithm is also called Edmund-Karp algorithm as the algorithm was provided in complete specification by Jack Edmonds and Richard Karp.
It works by creating augmenting paths i.e. paths from source to sink that have a non-zero flow. We pass the flow through the paths and we update the limits. This can lead to situation where we have no more moves left. That’s where the ‘undo’ ability of this algorithm plays a big role. In case of being stuck, we decrease the flow and open up the edge to pass our current substance.
Steps
- Set zero flow for all edges.
- While there is a path from source to sink do,
- Find the minimum weight on the path, let it be
limit. - For all edges (u, v) on the path do,
- Add
limitto flow from u to v. (For current move) - Subtract
limitfrom flow from v to u. (For undo in later move)
Evaluation
Time Complexity: O(V*E^2)
Python implementation
# Large number as infinity
inf = 1e10
def maximum_flow(graph, source, sink):
max_flow = 0
parent = bfs(graph, source, sink)
while path:
limit = inf
v = sink
while v != source:
u = parent[s]
path_flow = min(limit, graph[u][v])
v = parent[v]
max_flow += path_flow
v = sink
while v != source:
u = parent[v]
graph[u][v] -= path_flow
graph[v][u] += path_flow
v = parent[v]
path = bfs(graph, source, sink)
return max_flow