Hello @Shizbriz,
I will try to explain how I solved the exercise[4].
To be clear, I’m not a professional developer and I’m self taught. Also, the concepts/ideas/definitions used here are only a “just enough” approximation of the real ones and they are used in a way that make sense in the context of this explanation.
The approach used to solve the exercise is based on the book “How To Design Programs”[0][1](I tried to follow the techniques the best I could).
First, I will start with some definitions, in this explanation:
-
A recursive function is “a function that have a base case, a recursive case and solves the problem by calling himself from within his own code”
-
A base case is “an input that no require further tranformation, an input that breaks the chain of recursion (recursive calls)”
-
A recursive case is “an input that will be used (by a recursive function call) to break down a complex input into a simpler one (by applying some operation/process/tranformation)”
Fig. 0: code of the original question.
function rangeOfNumbers(startNum,endNum) {
if(endNum - startNum === 0 ) {
return [startNum];
} else {
let d = rangeOfNumbers(startNum, endNum - 1);
d.push(endNum);
return d;
}
}
Fig. 1: rangeOfNumbers input and output examples.
rangeOfNumbers(1,10); // [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
rangeOfNumbers(1, 9); // [1, 2, 3, 4, 5, 6, 7, 8, 9 ]
rangeOfNumbers(1, 8); // [1, 2, 3, 4, 5, 6, 7, 8 ]
rangeOfNumbers(1, 7); // [1, 2, 3, 4, 5, 6, 7 ]
rangeOfNumbers(1, 6); // [1, 2, 3, 4, 5, 6 ]
rangeOfNumbers(1, 5); // [1, 2, 3, 4, 5 ]
rangeOfNumbers(1, 4); // [1, 2, 3, 4 ]
rangeOfNumbers(1, 3); // [1, 2, 3 ]
rangeOfNumbers(1, 2); // [1, 2 ]
rangeOfNumbers(1, 1); // [1 ]
Fig. 1 is a series of examples of what we wants to acomplish with our function rangeOfNumbers. At the moment we don’t have any implementation (code). We are thinking.
At least for me, JS is difficult to read (we have some noise): we have words (function, rangeOfNumbers) and symbols ((,), //, ,) that are not part of the problem (are part of JS syntax). So, to remove that noise I use tables.
When making the table, I use the idea that functions are: something that takes an input(s), do some transfomation(s), and throw an output(s) ( input → transfomation → output).
Each input have a name, the output is just output:
Fig. 2:
| input (start , end) |
output |
| 1 , 10 |
1, 2, 3, 4, 5, 6, 7, 8, 9, 10 |
| 1 , 9 |
1, 2, 3, 4, 5, 6, 7, 8, 9 |
| 1 , 8 |
1, 2, 3, 4, 5, 6, 7, 8 |
| 1 , 7 |
1, 2, 3, 4, 5, 6, 7 |
| 1 , 6 |
1, 2, 3, 4, 5, 6 |
| 1 , 5 |
1, 2, 3, 4, 5 |
| 1 , 4 |
1, 2, 3, 4 |
| 1 , 3 |
1, 2, 3 |
| 1 , 2 |
1, 2 |
| 1 , 1 |
1 |
That’s better, less noise.
At this point we are trying to identify patterns, we look at Fig. 2 and we will try
identify: a base case and a recursive case.
For the base case we look at Fig. 2 and decide to use this example:
| input (start , end) |
output |
| 1 , 1 |
1 |
Why we will use this as a base case? because this is the simplest example in Fig.2, if we use this input we dont need to call the function multiple times (the output is a single value).
So, for us the example can be expressed this way:
| input (start , end) |
output |
| 1 , 1 |
1 |
| start and end are equals |
a single value, no need for a (recursive) function call |
For the recursive case we look at Fig. 2 and we try to find a way to express the output as a combination of: inputs plus some operation/process/transformation.
This part is difficult because we only have limited knowledge (we only know the inputs and ouput, we need to discover what operation/process/transformation the function apply. Remember a function is input -> transformation -> output)
At this point, we need to choose an example:
| input (start , end) |
output |
| 1 ,4 |
1, 2, 3,4 |
And try to express the example as a combination (input plus operations):
We can express the example using addition
| input (star, end) |
output |
| 1 , 4 |
1, 2, 3, 4 |
| 1 , 4 |
1, (1+1), (2+1), (3+1) |
We can express the example using subtraction
| input (start , end) |
output |
| 1 , 4 |
1, 2, 3, 4 |
| 1 , 4 |
1, (3-1), (4-1), (5-1) |
So, we just find that we can use 2 operations that will lets us to express the example as a combination:
1- addition
2- subtraction
But, we also need to find a way to use our named inputs:
Named inputs and addition:
| input (start, end) |
output |
| 1 , 4 |
1 , 2 , 3 , 4 |
| 1 , 4 |
start, (start) + 1, (start + 1) + 1, (start + 1 + 1) + 1 |
| 1 , 4 |
1 , ( 1 ) + 1, (1 + 1) + 1, (1 + 1 + 1) + 1 |
| 1 , 4 |
1 , 1 + 1, 2 + 1, 3 + 1 |
| 1 , 4 |
1 , 2 , 3 , 4 |
Named inputs and subtraction:
| input (start, end) |
output |
| 1 , 4 |
(end - 3), (end - 2), (end - 1), end |
| 1 , 4 |
(4 - 3), (4 - 2), (4 - 1), end |
| 1 , 4 |
1 , 2 , 3 , 4 |
We will use the representation: inputs and addition.
| input (start , end) |
output |
| 1 , 4 |
1 , 2 , 3 , 4 |
| 1 , 4 |
start, (start) + 1, (start + 1) + 1, (start + 1 + 1) + 1 |
| 1 , 4 |
1 , ( 1 ) + 1, (1 + 1) + 1, (1 + 1 + 1) + 1 |
| 1 , 4 |
1 , 1 + 1, 2 + 1, 3 + 1 |
| 1 , 4 |
1 , 2 , 3 , 4 |
We will replace the comma with a column, each (output) column is a function call
Fig. 3:
| input (start, end) |
output |
output |
output |
output |
| 1 , 4 |
start |
(start) + 1 |
(start + 1) + 1 |
(start + 1 +1) + 1 |
| 1 , 4 |
1 |
1 + 1 |
1 + 1 + 1 |
1 + 1 + 1 + 1 |
| 1 , 4 |
1 |
2 |
3 |
4 |
what we are trying to do here?
- We are replacing numbers(something infinite) with an named input/argument(finite) and an operation(finite)
- We are trying to determine what operation we need to apply to an input to get an specific ouput
what pattern we can identify?
- It seems that the next function call uses the previous input
An implementation:
I will be using this template, because a recursive function has one (or more) base case, a recursive case and calls himself.
function name(args) {
if(args) { // base case
} else { // recursive case
name(args); // calls himself
}
}
Function name:
function rangeOfNumbers(args) {
if(args) { // base case
} else { // recursive case
name(args); // calls himself
}
}
Function arguments (base case):
Base case:
| input (start, end) |
output |
| start and end are equals |
a single value, no need for a (recursive) function call |
Because we are using addition (start + 1) our base case is “start and end are equals”, not start === 1 and end === 1 (in our solution start increments and end is unchanged).
function rangeOfNumbers(start, end) {
if(start === end) { // base case
} else { // recursive case
name(args); // calls himself
}
}
Recursive case:
| input (start, end) |
output |
output |
output |
output |
| 1 , 4 |
start |
(start) + 1 |
(start + 1) + 1 |
(start + 1 +1) + 1 |
| 1 , 4 |
1 |
1 + 1 |
1 + 1 + 1 |
1 + 1 + 1 + 1 |
| 1 , 4 |
1 |
2 |
3 |
4 |
function rangeOfNumbers(start, end) {
if(start === end) { // base case
} else { // recursive case
// We will find later why this is start + 1 and not start + 1 , start + 1 + 1 ...
rangeOfNumbers(start + 1, end);
}
}
Returning an array:
I think this is the moment when most people get lost, they understand the solution but they are unaware of some abstractions of the language (JavaScript) in which they are implementing the solution.
if we look at Fig. 1 we can see that our example output an array:
rangeOfNumbers(1, 4); // [1, 2, 3, 4]
We will copy/paste most of the code of the original question (Fig.0) that implements the returning array step (because, this is something that most people do and will let’s ous to show why recursion is difficult to understand).
Following the code of the original question (Fig. 0), we will return an array from the base case:
- But the element inside will be
end
function rangeOfNumbers(start, end) {
if(start === end) { // base case
return [end]; // <- this
} else {
}
}
Following the code of the original question(Fig. 0), we will use a variable called d.
- But we will use our combination of inputs and addition
function rangeOfNumbers(start, end) {
if(start === end) { // base case
return [end];
} else {
let d = rangeOfNumbers(start + 1, end); // <- this
}
}
Following the code of the original question(Fig. 0), we will push one of our named inputs and we will return d.
function rangeOfNumbers(start, end) {
if(start === end) { // base case
return [end];
} else {
let d = rangeOfNumbers(start + 1, end); // recursive case
d.push(start); // <-- this
return d; // <-- this
}
}
Executing our implementation:
function rangeOfNumbers(start, end) {
if(start === end) { // base case
return [end];
} else {
let d = rangeOfNumbers(start + 1, end); // recursive case
d.push(start);
return d;
}
}
let result = rangeOfNumbers(1,4);
console.log(result);
Output: [ 4, 3, 2, 1 ]
Wait, I was expecting something different …
Before we talk about our expectations we need to think about some other misteries:
- The array: where does it come from?
- Why can I push
start to d?
- How exactly I’m using
start?
The call stack
According to wikipedia[2]
a stack is an abstract data type that serves as a collection of elements, with two main principal operations:
Push, which adds an element to the collection, and
Pop, which removes the most recently added element that was not yet removed.
The order in which elements come off a stack gives rise to its alternative name, LIFO (last in, first out)
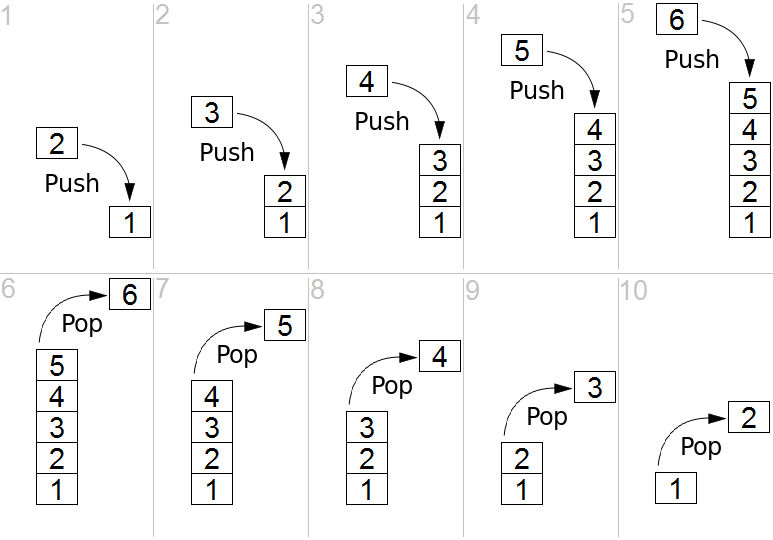
The last part is important:
The order in which elements come off a stack gives rise to its alternative name,
LIFO (last in, first out)
This is our solution (this is what we expected):
| input (start,end) |
output |
output |
output |
output |
| 1 , 4 |
start |
(start) + 1 |
(start + 1) + 1 |
(start + 1 +1) + 1 |
| 1 , 4 |
1 |
2 |
3 |
4 |
| input |
call |
call |
call |
call |
| rangeOfNumbers(1,4) |
rangeOfNumbers(1,4) |
rangeOfNumbers(2,4) |
rangeOfNumbers(3,4) |
rangeOfNumbers(4,4) |
rangeOfNumbers(1, 4); // [1,2,3,4]
This is what we got:
rangeOfNumbers(1, 4); // [4,3,2,1]
Why? because JavaScript has used the abstraction: call stack.
Now, the misteries
- The array: where does it come from?
From the call stack: last in, first out.
- Why can I push
start to d[3]?
When a function makes a nested call, the following happens:
The current function is paused.
The execution context associated with it is remembered in a special data structure called execution context stack.
The nested call executes.
After it ends, the old execution context is retrieved from the stack, and the outer function is resumed from where it stopped.
function rangeOfNumbers(start, end) {
if(start === end) { // base case
return [end]; // last in, first out
} else {
let d = rangeOfNumbers(start+1, end); // nested call
d.push(endNum); // d is the array from the base case
return d; // returning an array
}
}
- How exactly I’m using
start?
Your are using the (recursive) function calls to add 1 to the original start, to add 1 to start + 1… etc. This new value(of start) is pushed to d.
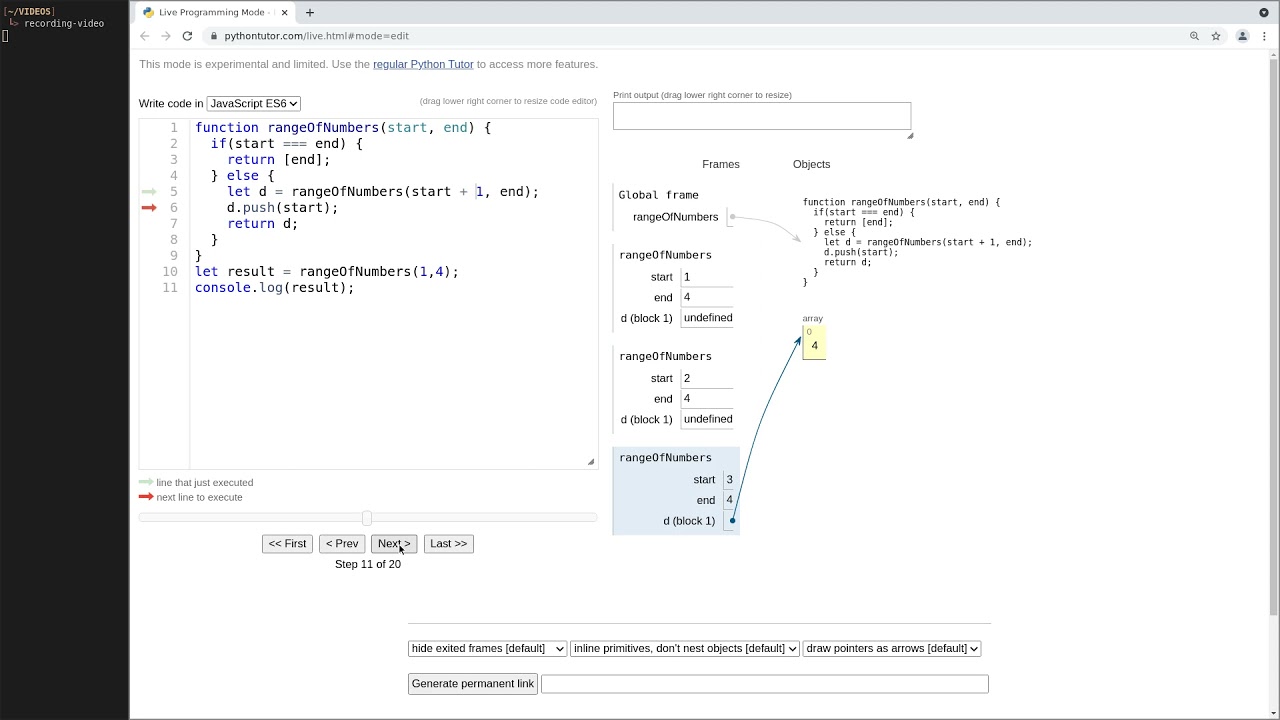
Is easier to understand with Python tutor
Now, the expectations
This is what we expected:
rangeOfNumbers(1,4)
rangeOfNumbers(2,4)
rangeOfNumbers(3,4)
rangeOfNumbers(4,4)
This how JS executed our code (Step 10 of 20):
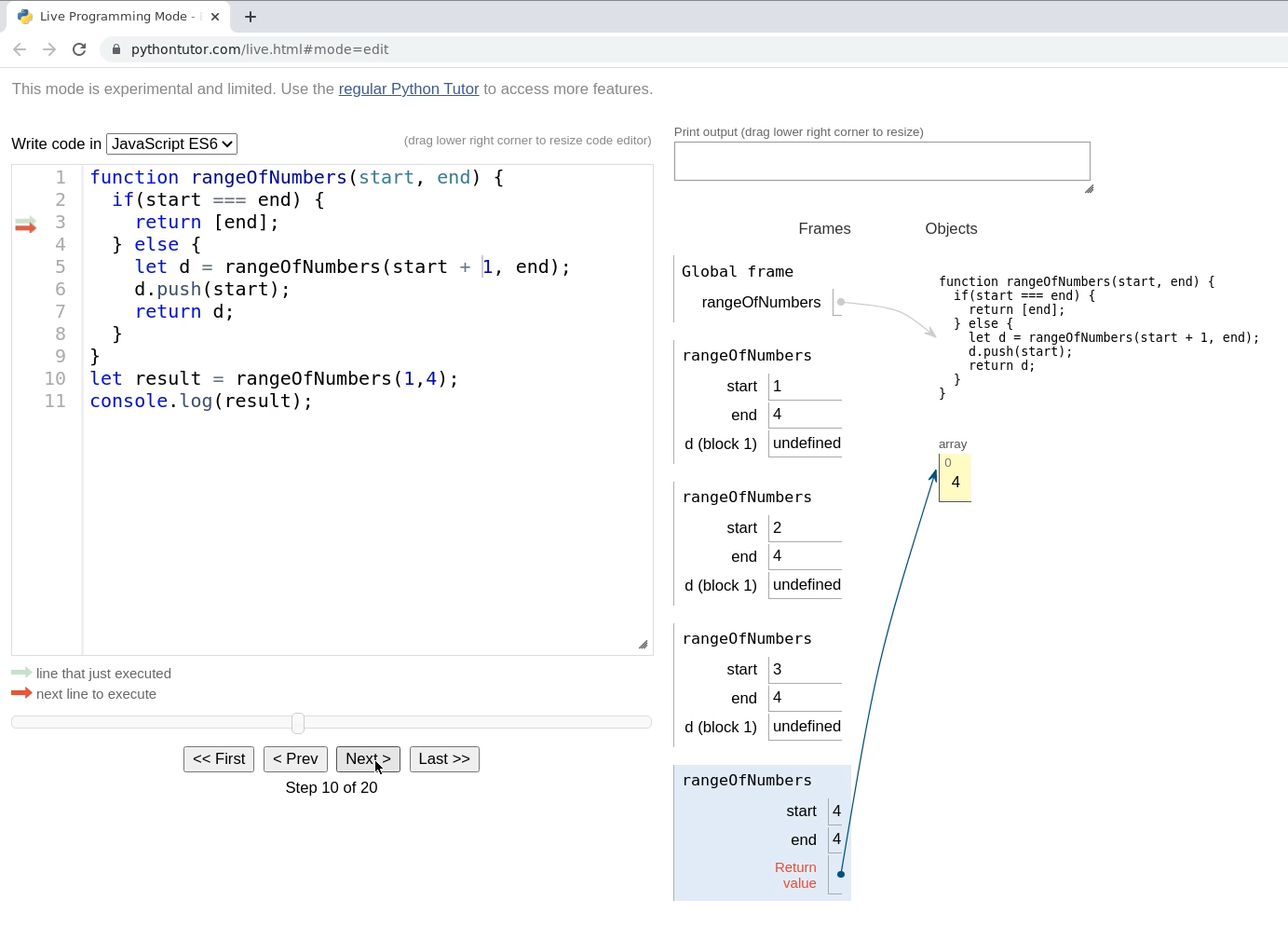
As you can see, up to this point we were right (we were right by 9 steps). This is the reason why I think that is not a good idea to identify an algorithm with a code implementation, our algorithm doesn’t have a call stack but our implementation has one.
A code implementation is NOT an algorithm. Also, the fact of not being aware of the call stack or don’t understand the call stack is not the same as don’t understand recursion … because recursion != implementation.
The process to find a solution is a series of multiple decisions. Just like a labyrinth, a path is taken(decision) and we have to follow it to find out where it leads ous.
Cheers and happy coding 
Notes:
[0] How to Design Programs, Second Edition
[1] Design Recipe for writing recursive programs
[2] Call stack - Wikipedia
[3] Recursion and stack
[4] Not exactly, is possible to ‘fix’ the code an get the output we wants but the idea of this post(?) is to shift the focus from “get the right answer for this exercise” to “I will use this exercise to find a recipe/workflow/mental framework that will let’s me analize more than one problem”